Hu Chen
INTRODUCTION
These days there is a lot of controversy regarding Caesarean deliveries in India. Some blame that medical fraternity and hospitals are deliberately doing more and more Caesarean deliveries. Let us explore how data science can help in this issue and making the decision about caesarean delivery or not with the help of an objective method i.e. machine learning.
DATASET
A sample of 80 women were collected who have either gone through caesarean delivery or normal delivery (M.Zain Amin, Amir Ali.'Performance Evaluation of Supervised Machine Learning Classifiers for Predicting Healthcare Operational Decisions'.Machine Learning for Operational Decision Making, Wavy Artificial Intelligence Research Foundation, Pakistan, 2018). This dataset is available on the following link---
https://archive.ics.uci.edu/ml/datasets/Caesarian+Section+Classification+Dataset
SUPPORT VECTOR MACHINE
We will do a classification model building with Support Vector Machine (SVM). Support Vector Machine is an algorithm which can be used for regression and classification. SVM can be used for linear and non-linear modelling. In this case study, we will try linear and nonlinear models for classification of Caesarean dataset.
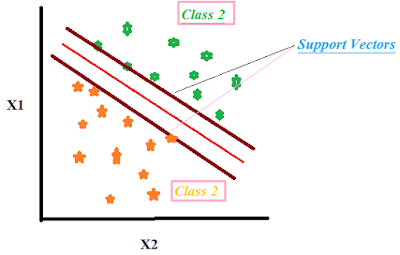
Figure 1 Support Vector Machine
In Figure 2, the theoretical framework of Support Vector is graphically represented. In Figure 2, there are two types of labels represented by green (Class2) and orange stars (Class1). On Y-axis, there is X1 variable and on X-axis, X2 variable and both are independent variables. The graph shows how each observation is distributed in 2 dimensions X1 and X2.
The Support Vectors are the imaginary lines that are drawn on the basis of the maximum distance possible from each class of data. The redline is the hyperplane which is obtained after rounds of optimizations. The redline hyperplane is the best plane in classifying the two classes. SVM algorithm finds the best hyperplane for the best classification. To know more SVM intuitively, click on the link below---
https://www.youtube.com/watch?v=efR1C6CvhmE
The machine learning model building with Support Vector Machine comprises of following steps---
A) Data Preparation & Exploratory Data Analysis
B) SVM Model Building & Prediction
Let's begin the appointment with Dr. SVM.
A) Data Preparation & Exploratory Data Analysis
In RStudio, we begin with setting the working directory and packages required.
>setwd(PATH_to_FILE)
>getwd()
>library(foreign)
>library(e1071)
>library(caret)
The dataset contains 80 observations and 6 variables. Out of six variables, five variables are attributes and one is a dependent variable. We give the name "ceas" to the file---
>ceas=read.arff("caesarian.csv.arff")
The attributes/independent variables are "age", "deliveryNumber", "BP", "deliveryTime" and "heartProblem". When we execute "str(ceas)" command, we find that all the variables are factor variable type. We need to convert them into the numeric format for model building and we will reove the parent variable---
>ceas$age=as.numeric(substr(ceas$Age,1,2))
>ceas$Age=NULL
>ceas$deliveryNumber=as.numeric(substr(ceas$`Delivery number`,1,1))
>ceas$`Delivery number`=NULL
>ceas$BP=as.numeric(substr(ceas$`Blood of Pressure`,1,1))
>ceas$`Blood of Pressure`=NULL
>ceas$deliveryTime=as.numeric(substr(ceas$`Delivery time`,1,1))
>ceas$`Delivery time`=NULL
>ceas$heartProblem=as.numeric(substr(ceas$`Heart Problem`,1,1))
>ceas$`Heart Problem`=NULL
Following summary statistics shows measures of central tendency and dispersion---
>summary(ceas)
let us understand distribution of each variable through the following tables---
> table(ceas$Caesarian)
0 1
34 46
Caesarian variable has two values 0 and 1. Value "0" represents that the delivery was non-caesarian and value "1" represents that the delivery was caesarian.
> table(ceas$age)
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 35 36 37 38 40
1 2 2 3 2 4 1 2 7 10 7 6 6 3 3 8 5 2 3 1 1 1
Exploring the dependencies of the Caesarian variable with other independent variables is important for model building. Hence, we analyze the impact of independent variables on the" caesarian" variable with the Chi-Squared test. The results of chi-squared tests are as follows---
> chisq.test(ceas$deliveryNumber, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$deliveryNumber and ceas$Caesarian
X-squared = 2.407, df = 3, p-value = 0.4923
> chisq.test(ceas$BP, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$BP and ceas$Caesarian
X-squared = 7.468, df = 2, p-value = 0.0239
> chisq.test(ceas$deliveryTime, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$deliveryTime and ceas$Caesarian
X-squared = 2.6379, df = 2, p-value = 0.2674
> chisq.test(ceas$heartProblem, ceas$Caesarian)
Pearson's Chi-squared test with Yates' continuity correction
data: ceas$heartProblem and ceas$Caesarian
X-squared = 8.5251, df = 1, p-value = 0.003503
B) SVM Model Building & Prediction
So, we begin with simple SVM model---
> model.svm=svm(Caesarian~.,data=ceas)
> summary(model.svm)
Call:
svm(formula = Caesarian ~ ., data = ceas)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.2
Number of Support Vectors: 65
( 29 36 )
Number of Classes: 2
Levels:
0 1
In the model summary, we can observe that, by default, model has selected nonlinear model i.e. SVM Kernal "radial". Model also optimized at Cost=1 and gamma=0.2. Model has done C-Classification. Number of Support Vectors are 65.
Let us predict the Caesarean type for data frame "ceas" with SVM model and then we evaluate the prediction with actual values---
> pred=predict(model.svm, ceas)
> table(ceas$Caesarian, pred)
pred
0 1
0 26 8
1 9 37
Following confusion matrix shows accuracy and other statistics of prediction by SVM model---
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 26 9
1 8 37
Accuracy : 0.7875
95% CI : (0.6817, 0.8711)
No Information Rate : 0.575
P-Value [Acc > NIR] : 5.404e-05
Kappa : 0.5669
Mcnemar's Test P-Value : 1
Sensitivity : 0.7647
Specificity : 0.8043
Pos Pred Value : 0.7429
Neg Pred Value : 0.8222
Prevalence : 0.4250
Detection Rate : 0.3250
Detection Prevalence : 0.4375
Balanced Accuracy : 0.7845
'Positive' Class : 0
Overall accuracy of the model is 78%.
Now, we apply cross-validation and SVM model together to see if there is any improvement in prediction or not. First, we try with linear SVM model---
>trctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 3)
>set.seed(3233)
>svm_Linear <- train(caes ~., data = ceas, method = "svmLinear",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneLength = 10)
Model summary is as follows---
>svm_Linear
Support Vector Machines with Linear Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results:
Accuracy Kappa
0.651918 0.3198123
Tuning parameter 'C' was held constant at a value of 1
Let us see, how it predicts the Caesarean variable---
> pred=predict(svm_Linear, newdata=ceas)
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 28 20
1 6 26
Accuracy : 0.675
95% CI : (0.5611, 0.7755)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.04356
Kappa : 0.3689
Mcnemar's Test P-Value : 0.01079
Sensitivity : 0.8235
Specificity : 0.5652
Pos Pred Value : 0.5833
Neg Pred Value : 0.8125
Prevalence : 0.4250
Detection Rate : 0.3500
Detection Prevalence : 0.6000
Balanced Accuracy : 0.6944
'Positive' Class : 0
We can see that the model accuracy of this model is lower than the simple model.
We can fine-tune model with hyperparameters C and gamma of the SVM model and let us see if model accuracy improves. We take the range of C values from 0.01 to 2.5.
>grid <- expand.grid(C = c(0,0.01, 0.05, 0.1, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2,5))
>set.seed(3233)
>svm_Linear_Grid <- train(caes ~., data = ceas, method = "svmLinear",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneGrid = grid,
tuneLength = 10)
>svm_Linear_Grid
> svm_Linear_Grid
Support Vector Machines with Linear Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results across tuning parameters:
C Accuracy Kappa
0.00 NaN NaN
0.01 0.5755291 0.0000000
0.05 0.5667328 0.1259469
0.10 0.6266534 0.2777531
0.25 0.6212963 0.2586232
0.50 0.6382275 0.2938355
0.75 0.6513228 0.3195901
1.00 0.6519180 0.3198123
1.25 0.6566799 0.3255291
1.50 0.6560847 0.3242667
1.75 0.6566799 0.3234376
2.00 0.6662037 0.3421381
5.00 0.6657407 0.3330852
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was C = 2.
> pred=predict(svm_Linear_Grid, newdata=ceas)
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 24 12
1 10 34
Accuracy : 0.725
95% CI : (0.6138, 0.819)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.003992
Kappa : 0.4416
Mcnemar's Test P-Value : 0.831170
Sensitivity : 0.7059
Specificity : 0.7391
Pos Pred Value : 0.6667
Neg Pred Value : 0.7727
Prevalence : 0.4250
Detection Rate : 0.3000
Detection Prevalence : 0.4500
Balanced Accuracy : 0.7225
'Positive' Class : 0
We can see that accuracy of the model has improved from 67% to 72% at C=2.
Now, let us apply nonlinear "radial" model again and see if model prediction improves or not.
> set.seed(3233)
> svm_Radial <- train(Caesarian ~., data = ceas, method = "svmRadial",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneLength = 10)
> svm_Radial
Support Vector Machines with Radial Basis Function Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results across tuning parameters:
C Accuracy Kappa
0.25 0.6093915 0.14372559
0.50 0.6707011 0.32367981
1.00 0.6381614 0.25688123
2.00 0.6212302 0.22192343
4.00 0.5928571 0.16922655
8.00 0.5871693 0.16469149
16.00 0.5913360 0.17885126
32.00 0.5556217 0.10723957
64.00 0.5172619 0.03346007
128.00 0.5010582 -0.00360852
Tuning parameter 'sigma' was held constant at a value of 0.2772785
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were sigma = 0.2772785 and C = 0.5.
>grid_radial <- expand.grid(sigma = c(0,0.01, 0.02, 0.025, 0.03, 0.04,
0.05, 0.06, 0.07,0.08, 0.09, 0.1, 0.25, 0.5, 0.75,0.9),
C = c(0,0.01, 0.05, 0.1, 0.25, 0.5, 0.75,
1, 1.5, 2,5))
>set.seed(3233)
>svm_Radial_Grid <- train(Caesarian ~., data = ceas, method = "svmRadial",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneGrid = grid_radial,
tuneLength = 10)
> pred=predict(svm_Radial_Grid, newdata=ceas)
> confusionMatrix(pred, ceas$Caesarian)
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 27 16
1 7 30
Accuracy : 0.7125
95% CI : (0.6005, 0.8082)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.007869
Kappa : 0.4314
Mcnemar's Test P-Value : 0.095293
Sensitivity : 0.7941
Specificity : 0.6522
Pos Pred Value : 0.6279
Neg Pred Value : 0.8108
Prevalence : 0.4250
Detection Rate : 0.3375
Detection Prevalence : 0.5375
Balanced Accuracy: 0.7231
'Positive' Class : 0
We can observe that cross-validation with different values of C and sigma degraded the model accuracy. We can try many other finetuning alternatives and other algorithms to improve the prediction. For now, we can select svm model with highest classification accuracy.
INTRODUCTION
These days there is a lot of controversy regarding Caesarean deliveries in India. Some blame that medical fraternity and hospitals are deliberately doing more and more Caesarean deliveries. Let us explore how data science can help in this issue and making the decision about caesarean delivery or not with the help of an objective method i.e. machine learning.
DATASET
A sample of 80 women were collected who have either gone through caesarean delivery or normal delivery (M.Zain Amin, Amir Ali.'Performance Evaluation of Supervised Machine Learning Classifiers for Predicting Healthcare Operational Decisions'.Machine Learning for Operational Decision Making, Wavy Artificial Intelligence Research Foundation, Pakistan, 2018). This dataset is available on the following link---
https://archive.ics.uci.edu/ml/datasets/Caesarian+Section+Classification+Dataset
SUPPORT VECTOR MACHINE
We will do a classification model building with Support Vector Machine (SVM). Support Vector Machine is an algorithm which can be used for regression and classification. SVM can be used for linear and non-linear modelling. In this case study, we will try linear and nonlinear models for classification of Caesarean dataset.
Figure 1 Support Vector Machine
In Figure 2, the theoretical framework of Support Vector is graphically represented. In Figure 2, there are two types of labels represented by green (Class2) and orange stars (Class1). On Y-axis, there is X1 variable and on X-axis, X2 variable and both are independent variables. The graph shows how each observation is distributed in 2 dimensions X1 and X2.
The Support Vectors are the imaginary lines that are drawn on the basis of the maximum distance possible from each class of data. The redline is the hyperplane which is obtained after rounds of optimizations. The redline hyperplane is the best plane in classifying the two classes. SVM algorithm finds the best hyperplane for the best classification. To know more SVM intuitively, click on the link below---
https://www.youtube.com/watch?v=efR1C6CvhmE
The machine learning model building with Support Vector Machine comprises of following steps---
A) Data Preparation & Exploratory Data Analysis
B) SVM Model Building & Prediction
Let's begin the appointment with Dr. SVM.
A) Data Preparation & Exploratory Data Analysis
In RStudio, we begin with setting the working directory and packages required.
>setwd(PATH_to_FILE)
>getwd()
>library(foreign)
>library(e1071)
>library(caret)
>library(ROCR)
The dataset contains 80 observations and 6 variables. Out of six variables, five variables are attributes and one is a dependent variable. We give the name "ceas" to the file---
>ceas=read.arff("caesarian.csv.arff")
The attributes/independent variables are "age", "deliveryNumber", "BP", "deliveryTime" and "heartProblem". When we execute "str(ceas)" command, we find that all the variables are factor variable type. We need to convert them into the numeric format for model building and we will reove the parent variable---
>ceas$age=as.numeric(substr(ceas$Age,1,2))
>ceas$Age=NULL
>ceas$deliveryNumber=as.numeric(substr(ceas$`Delivery number`,1,1))
>ceas$`Delivery number`=NULL
>ceas$BP=as.numeric(substr(ceas$`Blood of Pressure`,1,1))
>ceas$`Blood of Pressure`=NULL
>ceas$deliveryTime=as.numeric(substr(ceas$`Delivery time`,1,1))
>ceas$`Delivery time`=NULL
>ceas$heartProblem=as.numeric(substr(ceas$`Heart Problem`,1,1))
>ceas$`Heart Problem`=NULL
Following summary statistics shows measures of central tendency and dispersion---
>summary(ceas)
let us understand distribution of each variable through the following tables---
> table(ceas$Caesarian)
0 1
34 46
Caesarian variable has two values 0 and 1. Value "0" represents that the delivery was non-caesarian and value "1" represents that the delivery was caesarian.
> table(ceas$age)
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 35 36 37 38 40
1 2 2 3 2 4 1 2 7 10 7 6 6 3 3 8 5 2 3 1 1 1
In age variable, the range is 17 to 40.
> table(ceas$deliveryNumber)
1 2 3 4
41 27 10 2
The deliveryNumber tells about the number of times deliver incidents with the mother.
> table(ceas$BP)
0 1 2
20 40 20
The variable BP tells about the level of Blood Pressure. The 0,1 and 2 values represent low, normal and high respectively.
> table(ceas$deliveryTime)
0 1 2
46 17 17
The deliveryTime variable represents the type of delivery. The 0,1 and 2 values represent timely, premature and latecomer respectively.
> table(ceas$heartProblem)
0 1
50 30
The heartProblem variable tells about if there is heart problem to the pregnant woman or not. The 0 and 1 values represent apt and inept.
Exploring the dependencies of the Caesarian variable with other independent variables is important for model building. Hence, we analyze the impact of independent variables on the" caesarian" variable with the Chi-Squared test. The results of chi-squared tests are as follows---
> chisq.test(ceas$deliveryNumber, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$deliveryNumber and ceas$Caesarian
X-squared = 2.407, df = 3, p-value = 0.4923
> chisq.test(ceas$BP, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$BP and ceas$Caesarian
X-squared = 7.468, df = 2, p-value = 0.0239
> chisq.test(ceas$deliveryTime, ceas$Caesarian)
Pearson's Chi-squared test
data: ceas$deliveryTime and ceas$Caesarian
X-squared = 2.6379, df = 2, p-value = 0.2674
> chisq.test(ceas$heartProblem, ceas$Caesarian)
Pearson's Chi-squared test with Yates' continuity correction
data: ceas$heartProblem and ceas$Caesarian
X-squared = 8.5251, df = 1, p-value = 0.003503
We can observe the p-values of each chi.squared test. If p-value is less than 0.05 significance level, there is no evidence against the null hypothesis that both variables are independent. We can see that variables hearProblem and BP while deliveryNumber and deliveryTIme have no impact of on taking of decision of caesarean or no caesarean.
B) SVM Model Building & Prediction
Now, we are ready for model building. We are, here, going to use Support Vector Machine (SVM). The SVM technique is a very powerful technique in which we can build linear and nonlinear models. We will try different models in SVM for our case study.
So, we begin with simple SVM model---
> model.svm=svm(Caesarian~.,data=ceas)
> summary(model.svm)
Call:
svm(formula = Caesarian ~ ., data = ceas)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.2
Number of Support Vectors: 65
( 29 36 )
Number of Classes: 2
Levels:
0 1
In the model summary, we can observe that, by default, model has selected nonlinear model i.e. SVM Kernal "radial". Model also optimized at Cost=1 and gamma=0.2. Model has done C-Classification. Number of Support Vectors are 65.
Let us predict the Caesarean type for data frame "ceas" with SVM model and then we evaluate the prediction with actual values---
> pred=predict(model.svm, ceas)
> table(ceas$Caesarian, pred)
pred
0 1
0 26 8
1 9 37
Following confusion matrix shows accuracy and other statistics of prediction by SVM model---
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 26 9
1 8 37
Accuracy : 0.7875
95% CI : (0.6817, 0.8711)
No Information Rate : 0.575
P-Value [Acc > NIR] : 5.404e-05
Kappa : 0.5669
Mcnemar's Test P-Value : 1
Sensitivity : 0.7647
Specificity : 0.8043
Pos Pred Value : 0.7429
Neg Pred Value : 0.8222
Prevalence : 0.4250
Detection Rate : 0.3250
Detection Prevalence : 0.4375
Balanced Accuracy : 0.7845
'Positive' Class : 0
Overall accuracy of the model is 78%.
Now, we apply cross-validation and SVM model together to see if there is any improvement in prediction or not. First, we try with linear SVM model---
>trctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 3)
>set.seed(3233)
>svm_Linear <- train(caes ~., data = ceas, method = "svmLinear",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneLength = 10)
Model summary is as follows---
>svm_Linear
Support Vector Machines with Linear Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results:
Accuracy Kappa
0.651918 0.3198123
Tuning parameter 'C' was held constant at a value of 1
Let us see, how it predicts the Caesarean variable---
> pred=predict(svm_Linear, newdata=ceas)
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 28 20
1 6 26
Accuracy : 0.675
95% CI : (0.5611, 0.7755)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.04356
Kappa : 0.3689
Mcnemar's Test P-Value : 0.01079
Sensitivity : 0.8235
Specificity : 0.5652
Pos Pred Value : 0.5833
Neg Pred Value : 0.8125
Prevalence : 0.4250
Detection Rate : 0.3500
Detection Prevalence : 0.6000
Balanced Accuracy : 0.6944
'Positive' Class : 0
We can see that the model accuracy of this model is lower than the simple model.
We can fine-tune model with hyperparameters C and gamma of the SVM model and let us see if model accuracy improves. We take the range of C values from 0.01 to 2.5.
>grid <- expand.grid(C = c(0,0.01, 0.05, 0.1, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2,5))
>set.seed(3233)
>svm_Linear_Grid <- train(caes ~., data = ceas, method = "svmLinear",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneGrid = grid,
tuneLength = 10)
>svm_Linear_Grid
> svm_Linear_Grid
Support Vector Machines with Linear Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results across tuning parameters:
C Accuracy Kappa
0.00 NaN NaN
0.01 0.5755291 0.0000000
0.05 0.5667328 0.1259469
0.10 0.6266534 0.2777531
0.25 0.6212963 0.2586232
0.50 0.6382275 0.2938355
0.75 0.6513228 0.3195901
1.00 0.6519180 0.3198123
1.25 0.6566799 0.3255291
1.50 0.6560847 0.3242667
1.75 0.6566799 0.3234376
2.00 0.6662037 0.3421381
5.00 0.6657407 0.3330852
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was C = 2.
> pred=predict(svm_Linear_Grid, newdata=ceas)
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 24 12
1 10 34
Accuracy : 0.725
95% CI : (0.6138, 0.819)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.003992
Kappa : 0.4416
Mcnemar's Test P-Value : 0.831170
Sensitivity : 0.7059
Specificity : 0.7391
Pos Pred Value : 0.6667
Neg Pred Value : 0.7727
Prevalence : 0.4250
Detection Rate : 0.3000
Detection Prevalence : 0.4500
Balanced Accuracy : 0.7225
'Positive' Class : 0
We can see that accuracy of the model has improved from 67% to 72% at C=2.
Now, let us apply nonlinear "radial" model again and see if model prediction improves or not.
> set.seed(3233)
> svm_Radial <- train(Caesarian ~., data = ceas, method = "svmRadial",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneLength = 10)
> svm_Radial
Support Vector Machines with Radial Basis Function Kernel
80 samples
5 predictor
2 classes: '0', '1'
Pre-processing: centered (5), scaled (5)
Resampling: Cross-Validated (10 fold, repeated 3 times)
Summary of sample sizes: 71, 72, 72, 72, 73, 73, ...
Resampling results across tuning parameters:
C Accuracy Kappa
0.25 0.6093915 0.14372559
0.50 0.6707011 0.32367981
1.00 0.6381614 0.25688123
2.00 0.6212302 0.22192343
4.00 0.5928571 0.16922655
8.00 0.5871693 0.16469149
16.00 0.5913360 0.17885126
32.00 0.5556217 0.10723957
64.00 0.5172619 0.03346007
128.00 0.5010582 -0.00360852
Tuning parameter 'sigma' was held constant at a value of 0.2772785
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were sigma = 0.2772785 and C = 0.5.
> pred=predict(svm_Radial, newdata=ceas)
> confusionMatrix(as.factor(pred), as.factor(ceas$Caesarian))
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 25 8
1 9 38
Accuracy : 0.7875
95% CI : (0.6817, 0.8711)
No Information Rate : 0.575
P-Value [Acc > NIR] : 5.404e-05
Kappa : 0.5635
Mcnemar's Test P-Value : 1
Sensitivity : 0.7353
Specificity : 0.8261
Pos Pred Value : 0.7576
Neg Pred Value : 0.8085
Prevalence : 0.4250
Detection Rate : 0.3125
Detection Prevalence : 0.4125
Balanced Accuracy : 0.7807
'Positive' Class : 0
We can see that accuracy of "radial" model is 79% which is higher than linear models. Let us see if finetuning of "radial" model improves the model or not by changing values of C and Sigma---
>grid_radial <- expand.grid(sigma = c(0,0.01, 0.02, 0.025, 0.03, 0.04,
0.05, 0.06, 0.07,0.08, 0.09, 0.1, 0.25, 0.5, 0.75,0.9),
C = c(0,0.01, 0.05, 0.1, 0.25, 0.5, 0.75,
1, 1.5, 2,5))
>set.seed(3233)
>svm_Radial_Grid <- train(Caesarian ~., data = ceas, method = "svmRadial",
trControl=trctrl,
preProcess = c("center", "scale"),
tuneGrid = grid_radial,
tuneLength = 10)
> pred=predict(svm_Radial_Grid, newdata=ceas)
> confusionMatrix(pred, ceas$Caesarian)
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 27 16
1 7 30
Accuracy : 0.7125
95% CI : (0.6005, 0.8082)
No Information Rate : 0.575
P-Value [Acc > NIR] : 0.007869
Kappa : 0.4314
Mcnemar's Test P-Value : 0.095293
Sensitivity : 0.7941
Specificity : 0.6522
Pos Pred Value : 0.6279
Neg Pred Value : 0.8108
Prevalence : 0.4250
Detection Rate : 0.3375
Detection Prevalence : 0.5375
Balanced Accuracy: 0.7231
'Positive' Class : 0
We can observe that cross-validation with different values of C and sigma degraded the model accuracy. We can try many other finetuning alternatives and other algorithms to improve the prediction. For now, we can select svm model with highest classification accuracy.